Легко?
Многие математические открытия могут быть сделаны или поняты только путем глубокого изучения сложных деталей символов и уравнений. Но иногда достаточно того, чему каждый ребенок учится в школе.

Все учились в школе, как делить 1 на 7. Единственное, что на первый взгляд кажется примечательным в этом результате, это то, что десятичные разряды повторяются снова и снова. Это показано в формуле горизонтальной линией; но вы можете записать результат как 0,142857142857….
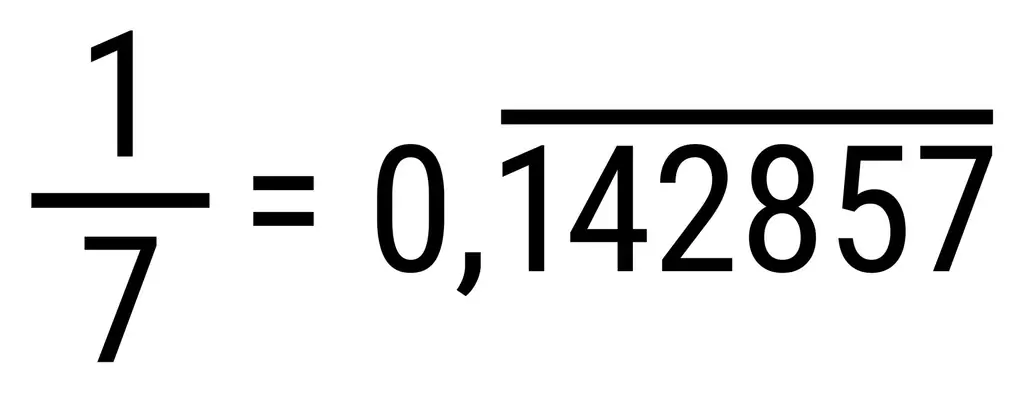
Если вы разделите два целых числа друг на друга, вы всегда получите результат этой формы. Либо результатом вычисления является целое число, либо есть остаток, который затем генерирует периодически повторяющуюся последовательность цифр в последовательности десятичных разрядов. Только иррациональные числа (например, число пи или квадратный корень из 2) не имеют закономерностей после запятой и по определению не могут быть представлены как частное двух целых чисел.
Итак, до этого момента в делении 1 на 7 нет ничего необычного. Это изменится, если вы внимательно посмотрите на число 142 857. Потому что это так называемое циклическое число. Так называют все n-значные натуральные числа, произведение которых с числами от 1 до n содержит те же цифры, что и исходное число. Кроме того, эти цифры не должны появляться в произвольном порядке, а должны циклически переставляться: их можно только сдвигать, но не смешивать.
Например, если умножить 142 857 на 2, получится 285 714. Произведение на 3 равно 428 571, умножение на 4 равно 571 428 и так далее. Но вы также можете посмотреть на это иначе: результат деления всех целых чисел от 1 до 6 на 7 всегда возвращает одни и те же повторяющиеся шесть цифр после запятой. Последовательность также всегда одинакова; За 1 всегда следует 4, за 4 всегда следует 2 и так далее. Единственная разница между различными делениями - это число, с которого начинается период (например, 2, деленное на 7, дает 0,285714285714…).
Американский математик Леонард Диксон смог показать, что все циклические числа являются периодами чисел, которые определяются из обратной величины простых чисел. Такие простые числа называются генераторными числами, а 7 - наименьшее из них. Если оставить в стороне тривиальные циклические числа (числа от 0 до 9), то 142 857 - наименьшее из циклических чисел.
В общем случае простое число p (в десятичной системе) является образующим числом тогда и только тогда, когда для натуральных чисел n между 0 и p -1 число 10 -1 не кратно p. Кроме того, 10p-1-1 должно быть кратно p.
После 7 следующее порождающее число - 17. Циклическое число, вычисленное из этого, уже имеет 16 цифр и равно 0588235294117647. Среди простых чисел, меньших 100, есть восемь других порождающих чисел: 19, 23., 29, 47, 59, 61 и 97. Однако при всех этих и следующих порождающих числах результирующее циклическое число начинается с нуля. В самом деле, если не допускать таких лидирующих нулей в циклических числах, то 142 857 - единственное нетривиальное циклическое число в десятичной системе, а 7 - единственное порождающее число.
И это довольно удивительный результат простого деления 1 на 7.
