Кеплер, Ньютон и МКС
400 лет назад у людей были абстрактные мысли о фундаментальной природе космоса. Это знание, которое в то время было чисто теоретическим, теперь определяет нашу жизнь и нашу повседневную жизнь.

Люди, незнакомые с ночным небом, часто удивляются тому, что там можно увидеть. Но это также может случиться с кем-то вроде меня, кто профессионально занимается астрономией. Например, когда Международная космическая станция хорошо видна и ярко движется по небу ранним вечером. Я тоже всегда под впечатлением от этого зрелища.
Однако я не звоню в ближайшую обсерваторию, чтобы сообщить о наблюдении НЛО (что люди делают регулярно), а думаю об Иоганне Кеплере, Исааке Ньютоне и этой математической формуле:
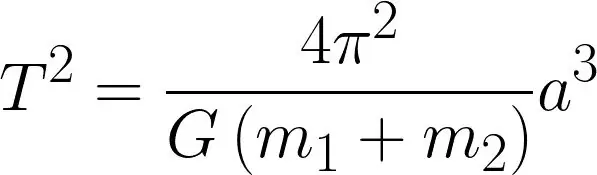
Это в несколько незнакомой форме третий из трех знаменитых законов Кеплера для описания орбит планет. Первые два можно сформулировать достаточно просто, безо всякой математики: небесные тела обращаются вокруг Солнца не по кругам, а по эллиптическим орбитам. А когда небесное тело приближается к солнцу по своей эллиптической орбите, оно движется быстрее, чем когда оно далеко от него.
Но третий закон Кеплера всегда немного необычен. В школе его обычно преподают в следующей формулировке: «Квадраты орбитальных времен находятся в том же отношении, что и кубы больших полуосей». Это звучит довольно абстрактно и определенно математически, но на самом деле это означает не что иное, как: чем больше орбита небесного тела, то есть чем больше его среднее расстояние от Солнца, тем больше времени ему требуется для одного оборота.
Но эта почти чрезмерно упрощенная формулировка на самом деле не отдает должного работе Иоганна Кеплера - что особенного в его третьем законе, так это то, что очевидный факт может быть выражен математически: что планета длиннее, чем вы вращаетесь вокруг Солнца, когда его орбита больше.
Кеплер был очень близок
Третий закон Кеплера тесно связан с законом всемирного тяготения Исаака Ньютона; можно даже вывести его непосредственно из него. На самом деле Кеплер был на пороге открытия того, что Ньютон открыл всего несколько десятилетий спустя: третий закон Кеплера в показанной выше форме детализирует связь между ними..
В своей первоначальной версии закона Кеплер мог указать только отношения, а не абсолютные значения. В то время они также не были известны, поскольку точные расстояния между планетами можно было измерить только намного позже его времени. Однако, зная закон всемирного тяготения и задействованные массы небесных тел, можно вычислить и абсолютные значения по закону Кеплера.
Подставляя в формулу, например, гравитационную постоянную G, массу m1 Земли и массу m2 Международной космической станции - около 420 тонн - и учитывая, что она находится примерно в 6780 километрах от центра Земли (это соответствует «большой оси» а в формуле), то можно вычислить период ее обращения Т непосредственно вокруг нашей планеты: 5556 секунд или 92,6 минуты.
Так что, если я увижу космическую станцию, летящую над головой в определенный момент времени, у меня есть хорошие шансы увидеть ее снова примерно через 90 минут. С тем ограничением, что условия наблюдения, преобладающие в конкретном месте на Земле, также зависят от нескольких других факторов.
Когда много веков назад Иоганн Кеплер и Исаак Ньютон думали о движении небесных тел, они хотели понять, как устроена Вселенная. Вряд ли они могли себе представить, что их знания, которые в то время были абстрактными, будут сегодня доминировать в нашем современном мире. Ее законами определяется не только траектория МКС, но и различных навигационных и телевизионных спутников. Математика Иоганна Кеплера сегодня повсюду!
