Архетипическое «мигание светодиодом» - отличный начальный проект на любой платформе, но как только ошибка появляется, это быстро превращается в исследование того, сколько именно светодиодов может управлять данный микроконтроллер. И это часто приводит к Чарлиплексингу. Быстрый поиск дает много копий таблицы, описывающей, сколько светодиодов может управляться заданным количеством контактов, но это всего лишь самый элементарный способ описания. Еще в 2013 году [M Rule] разработал хитрый прием для описания количества светодиодных матриц, которые могут управляться массивом Charlieplexed заданного размера, что делает этот процесс намного более интуитивным. Пост может быть старым, но мы обещаем, что метод все еще свеж.
[M Rule] специально стремился управлять этими большими дешевыми одноцветными светодиодными матрицами, которые часто используются для создания знаков с прокруткой и тому подобного. Эти части обычно представляют собой матрицу светодиодов с рядом общих катодов и одним общим анодом. Внутренне они совершенно тупые и могут управляться сканированием строк/столбцов или любым другим способом, которым можно управлять типичной матрицей. Вопрос в том, учитывая известные размеры матриц, сколько из них можно подключить с помощью определенного числа штифтов привода светодиодов Charlieplexed?
Первый шаг - визуализировать одномерный массив доступных контактов в виде двумерной матрицы, как показано справа. Обратите внимание, что каждый пронумерованный вывод одинаков на X и Y, поэтому черная зона исключения недопустимых комбинаций выводов рассекает график (вы не можете управлять светодиодом, подключенным к одному выводу дважды). Хитрость, если бы кто-то сказал, что он находится в одном месте, заключался бы в том, чтобы назвать ось анодом и катодом, представляя две «ориентации», в которые могут быть вставлены приводные штифты. С учетом этой диаграммы [Правило М] вы можете просто поместить матрицу в массив. Если он находится за пределами зоны отчуждения, он может управляться этими штифтами!
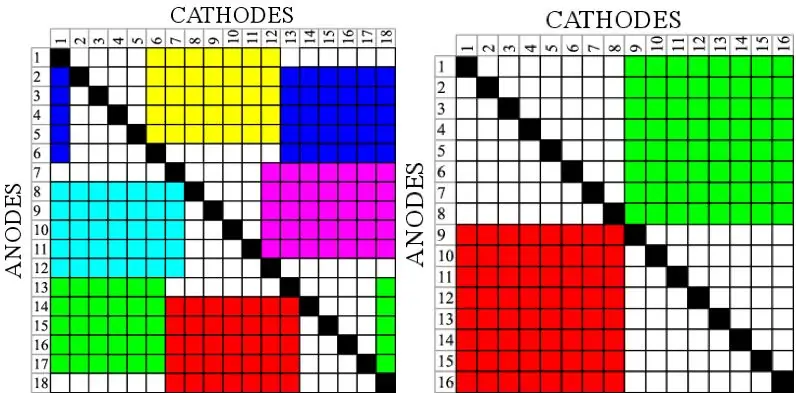
Слева показано, как это выглядит с двумя матрицами 8×8, одна из которых подключена между контактами 1-8 и 9-16, а другая - между 9-16 и 1-8. Это не очень интересно, но этот метод одинаково хорошо работает с одиночными светодиодами и матрицей любого размера, включая 7-сегментные дисплеи. Кроме того, пока элемент не перекрывает сам себя, он может закругляться по краям, что приводит к некоторым диким визуальным эффектам, например, к 14 светодиодам RGB на семи контактах справа.
Самые экстремальные примеры довольно экзотичны. Проверьте пост [M Rule] о жемчужине короны; 18 контактов для управления шестью модулями 5×7, шестью 7-сегментными дисплеями, 12 одиночными светодиодами и 18 кнопками!
Если эта диаграмма с цветовой кодировкой кажется вам знакомой, возможно, вы помните прекрасную диаграмму [openmusiclabs], описывающую способы сканирования многих кнопок. Или наше освещение еще одного приема матричной топологии [M Rule] несколько недель назад.