Как пробка возникает из ниоткуда?
Особенно раздражают пробки без конкретной причины. Почему они особенно несправедливы и в то же время неизбежны, можно объяснить математически.

Я предпочитаю передвигаться на велосипеде. Я езжу на поезде на дальние расстояния, но я очень доволен своим безмоторным транспортным средством для более коротких поездок по городу и окрестностям. Раньше я водил машину, но я не был за рулем автомобиля более десяти лет и совершенно не скучаю по этому. Особенно, когда я неторопливо проезжаю мимо очередей машин.
Для людей в машинах такая пробка, конечно, очень раздражает. Тем более, что нет даже конкретной причины. По-прежнему понятно, что движение останавливается в случае аварии или строительной площадки. Но часто он возвращается без каких-либо событий. Такая «пробка из ниоткуда» или «фантомная пробка» особенно раздражает, но, по крайней мере, математически объяснима. В 1992 году физики Кай Нагель и Майкл Шрекенберг опубликовали модель, которая позволила им объяснить образование фантомных пробок. Это можно резюмировать следующим математическим уравнением:
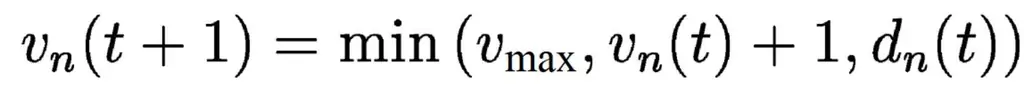
В системе, известной сегодня как «модель Нагеля-Шрекенберга», можно представить себе конкретное количество автомобилей, заданное числом «n». Каждый занимает определенное место на дороге, определяемое размером транспортных средств. У каждого автомобиля есть определенная скорость (v), которая не должна превышать максимально допустимую скорость (v max). Дальнейшее развитие трафика описывается четырьмя простыми правилами, которые сводятся к приведенной выше формуле и ясно описываются следующим образом:
- Если автомобиль еще не движется с максимальной скоростью в текущий момент времени (t), он увеличивает свою текущую скорость на единицу до следующего момента времени (t +1). Этот шаг описывает желание водителя двигаться как можно быстрее.
- Если пространство перед автомобилем, описываемое параметром d (t), слишком мало для текущей скорости, то оно тормозит. Этот шаг посвящен описанию поведения водителей, которые тормозят, чтобы избежать аварий.
- Это важный шаг в модели: случайным образом транспортное средство начнет «раскачиваться» и немного замедлится.
- Все транспортные средства продолжают двигаться со скоростями, рассчитанными в шагах с 1 по 3, и расчет начинается заново.
Объяснение образования фантомных заторов находится в шаге 3 модели Нагеля-Шрекенберга. Потому что ни одно транспортное средство не всегда движется с абсолютно постоянной скоростью. Даже если больше ничего не происходит, машина иногда становится немного быстрее, а иногда немного медленнее. Часто «бездельничанье» также вызвано чрезмерной реакцией, например, когда водитель тормозит сильнее, чем это было бы необходимо, чтобы предотвратить наезд сзади на впереди идущее транспортное средство. Или водители отвлекаются на телефонные звонки, разговоры или просмотр чего-то на обочине.
Когда дорога пуста или на ней мало машин, замедление движения не влияет на транспортный поток. Однако существует «критическая плотность», выше которой безделье одной машины может повлиять на все последующие. Там, где первый бездельник замедляется лишь немного, следующему транспортному средству приходится замедляться больше, автомобилю позади еще больше - и так далее. Пока транспортное средство не остановится полностью и из ниоткуда не возникнет пробка.
Модель Нагеля-Шрекенберга также показывает присущую таким фантомным пробкам несправедливость: человек, устроивший пробку, ничего не замечает. Для проявления эффекта требуется некоторое время. К тому времени, когда остальная часть движения останавливается и начинает беспокоиться о неожиданной и нежелательной остановке, транспортное средство, вызвавшее пробку из ниоткуда, уже давно уехало.
Хотя математические модели специалистов по дорожному движению могут объяснить, почему на наших дорогах возникают пробки, они редко могут их предотвратить. Вот почему я продолжаю ездить на велосипеде и, в конце концов, обычно добираюсь до места назначения быстрее, чем автомобильные пробки.
