Кристиан Гольдбах (1690-1764): Человек, который любил простые числа
Любое четное число больше 2 является суммой двух простых чисел. Гипотеза Гольдбаха - одна из самых известных нерешенных проблем математики.

Одна из самых известных недоказанных гипотез в теории чисел:
Любое четное число больше 2 можно представить в виде суммы двух простых чисел.
Ученый Кристиан Гольдбах поделился этим простым математическим утверждением со своим другом по переписке Леонардом Эйлером в 1742 году в качестве предположения. (В оригинальной версии по-прежнему говорится: каждое натуральное число, большее 2, может быть представлено в виде суммы трех простых чисел, вследствие чего в то время число 1 все еще считалось простым числом.)
Все попытки доказать эту теорему пока не увенчались успехом. Даже предложение награды в 1 миллион долларов мало что дало. В 1966 году Чэнь Цзинжунь (1933-1996), ученик Хуа Луогэна (1910-1985), самого известного китайского математика 20 века, достиг «наилучшего приближения» гипотезы Гольдбаха на сегодняшний день. Чэнь Цзинжунь смог доказать, что любое достаточно большое четное число можно представить в виде суммы простого числа и другого числа, имеющего не более двух простых делителей.
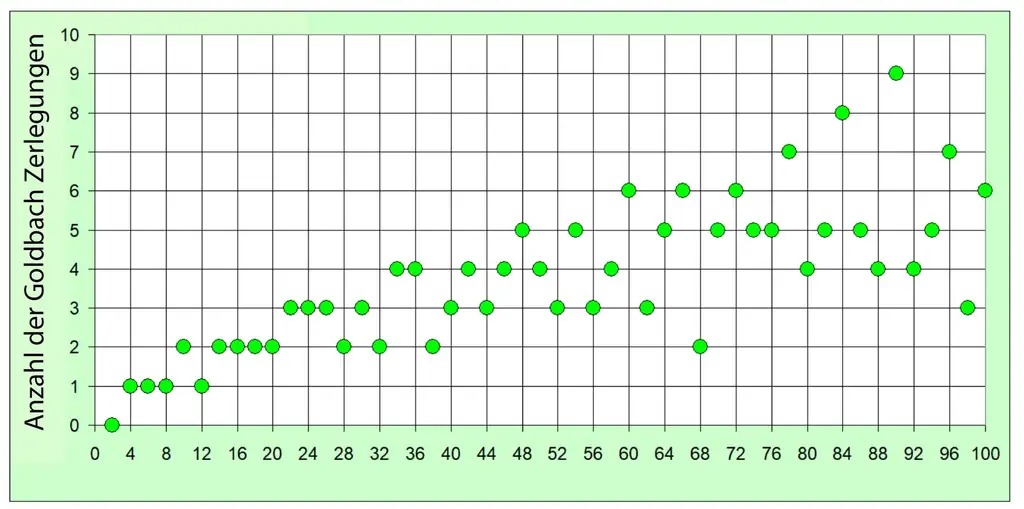
Среди первых четных чисел есть такие, которые имеют только разложение Гольдбаха (4=2 + 2; 6=3 + 3; 8=3 + 5; 12=5 + 7).
Для больших четных чисел существует «тенденция» к увеличению числа возможностей, но тогда всегда есть число, которое имеет лишь несколько разложений, например, 98=19 + 79=31 + 67=37 + 61.
Кристиан Гольдбах, сын протестантского пастора, вырос в Кенигсберге (Восточная Пруссия), где он учился в средней школе и университете. Во время учебы он в основном занимается юриспруденцией и медициной. Более длительные учебные поездки между 1710 и 1724 годами привели его во многие европейские города, где он встретил многих важных математиков: в Лейпциге он посетил Готфрида Лейбница, в Лондоне он обменялся идеями с Авраамом де Муавром, в Оксфорде он встретил Николая Бернулли (I) и в Венеции. чей двоюродный брат Николай II, который устанавливает связь со своим младшим братом Даниилом (все племянники Якова и Иоганна Бернулли).
Вернувшись в Кенигсберг в 1724 году, он познакомился с двумя приглашенными учеными, немецким философом Георгом Бернхардом Бильфингером и швейцарским математиком Якобом Германом, которые направлялись в Санкт-Петербург, чтобы основать там академию - на основе Берлинская модель построения науки. В следующем году Гольдбах подал заявку на должность президента новой академии, но сначала получил отказ, но затем в конце 1725 года был назначен на кафедру математики и истории.
В студенческие годы Гольдбах почти не занимался математикой; однако после встречи с Лейбницем его интерес к математическим темам возрос, о чем свидетельствует, например, статья о бесконечных рядах в «Acta eruditorum».
С момента основания академии Гольдбах принял должность секретаря и выполнял эту координирующую функцию до 1727 года, когда он был назначен воспитателем молодого царя Петра II (внука Петра Великого). Царица Екатерина I постановила, что ее единственный двенадцатилетний внук должен унаследовать царский престол. В борьбе за фактическую власть в стране между соперничающими генералами Меньшиковым и Долгоруковым Москва на время снова становится столицей России, так что Гольдбаху приходится двигаться вместе с двором. Когда пять лет спустя молодой царь умер, Гольдбах остался в Москве до тех пор, пока новая царица Анна Ивановна не вернула двор в Петербург в 1732 году. После смерти Анны Ивановны в 1740 году ее сын, которому было всего несколько недель от роду, был временно провозглашен царем, пока Елизавета, дочь Петра Великого, не захватила власть. Как один из немногих при дворе, Кристиан Гольдбах пережил все эти смены правительства без ущерба.
У Гольдбаха все меньше и меньше времени беспокоиться о математике; В 1729 г. и снова в 1732 г. он опубликовал статью о бесконечных рядах. Его административное бремя управления академией растет с каждым годом, пока он, наконец, не попросит сократить свои обязанности.
Гольдбах даже полностью освобожден от своих академических обязанностей в 1740 году; потому что новая царица продвинула красноречивого космополита на важную должность в министерстве иностранных дел, что помогло ему в последующие годы обрести большое богатство и землевладение. Математика остается его любимым занятием, и в лице Леонарда Эйлера у него есть очень компетентный корреспондент.
Леонард Эйлер и Христиан Гольдбах лично познакомились друг с другом в 1727 году, когда Эйлер начал преподавать в Санкт-Петербурге. Во время пребывания Гольдбаха в Москве начался оживленный обмен письмами между двумя учеными, продолжавшийся более 35 лет. Внутриполитические потрясения 1740/41 г. побудили Эйлера принять вызов в Берлин, где он занял должность директора математического класса Прусской академии наук.
Эти двое говорят, в частности, о проблемах теории чисел. Гольдбаха интересует не только приведенное выше предположение. В ходе своих исследований он дает много предложений Эйлеру, который может решить ряд следующих задач:
- Представимость нечетных натуральных чисел: Гольдбах предполагает, что каждое нечетное натуральное число (больше 17) может быть представлено в виде 2 · n 2 + p, где p - простое число равно (19=2 12 + 17=2 22 + 11; 21=2 12 + 19=2 22 + 13=2 32 + 3, 23=2 3 2+ 5;25=2 12 + 23=2 22 + 17=2 3 2+ 7 27=2 22 + 19 29=2 32 + 11;…). Эйлер исследует нечетные числа до 999; Гольдбах даже проверяет предположение до числа 2499; В 1856 г. Мориц Штерн нашел два контрпримера (5777 и 5993); неизвестно, существуют ли другие контрпримеры.
- Свойства чисел Ферма (натуральные числа вида F=\(2^{2^n}) + 1, которые, как подозревал Ферма, всегда касаются сделок с простыми числами); В 1732 году Эйлер обнаружил, что F5=4 294 967 297 не является простым, поскольку число делится на 641. Сегодня предполагается, что только числа от F0 до F4 являются простыми числами.
- Свойства чисел Мерсенна (натуральные числа вида M=2 n - 1) и совершенных чисел (натуральные числа, сумма истинных делителей равна самому числу): Евклид уже показал, что каждое натуральное число вида 2 n -1 · (2 n - 1) совершенно, если 2 n - 1 простое число; Эйлер доказывает, что верна и обратная теорема.
- Полиномы, производящие простые числа: В 1772 году Эйлер нашел многочлен n 2 + n + 41, в котором натуральные числа n=0, 1, 2, 3, …, 39 все простые числа.
Представимость натуральных чисел в виде суммы квадратных чисел, кубических чисел, вообще k-х степеней, определение наименьшего числа g(k) необходимых слагаемых, где: g(2)=4 (т.е. называется ларанжским четырехугольным предложением); г(3)=9; г(4)=17; g(5)=37 (доказано Чен Цзинжуном в 1964 г.). Обобщение называется проблемой Варинга (по Эдварду Варингу, 1736-1798)
- Исследование бесконечного ряда обратных степеней: Гольдбах исследует натуральные числа больше 1, которые можно записать в виде степеней, т. е. 4=22, 8=2 3, 9=32, 16=24 и 16=42 , 25=52, 27=33 и так далее. Он предполагает, что бесконечная сумма обратных величин степеней, уменьшенных на 1 (без удвоений типа 16), равна 1: \[sum_k \frac{1}{k-1}=\frac{1}{3} +\frac {1}{7} +\frac{1}{8} + \frac{1}{15} + \frac{1}{24} + \frac{1}{26} + …=1.] Эйлер удается доказать эту так называемую теорему Гольдбаха-Эйлера в 1737 году (хотя его расчет с бесконечными суммами не является «строгим» доказательством по сегодняшним стандартам).
Гольдбах не доживает до возвращения Эйлера в Россию (1766 г.); В 1764 г. уважаемый ученый и государственный деятель скончался в Москве в возрасте 74 лет.
