Сложная арифметика чисел
Глава 2 - Комплексные числа
Поскольку комплексные числа являются законными математическими объектами, как и скалярные числа, они могут быть добавлены, вычтены, умножены, разделены, квадратичны, перевернуты и т. Д., Как и любой другой вид числа. Некоторые научные калькуляторы запрограммированы на непосредственное выполнение этих операций на двух или более сложных числах, но эти операции также могут выполняться «вручную». В этом разделе будет показано, как выполняются основные операции. Настоятельно рекомендуется оснастить себя научным калькулятором, способным легко выполнять арифметические функции на комплексных числах. Это сделает ваше исследование схемы переменного тока более приятным, чем если бы вы были вынуждены делать все вычисления более длинным способом.
Сложение и вычитание с комплексными числами в прямоугольной форме легко. Для добавления просто добавьте реальные компоненты комплексных чисел, чтобы определить реальную компоненту суммы, и добавьте мнимые компоненты комплексных чисел, чтобы определить мнимую составляющую суммы:
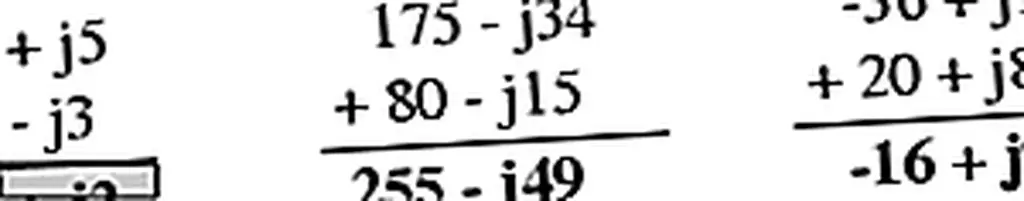
Вычитая комплексные числа в прямоугольной форме, просто вычтите действительную составляющую второго комплексного числа из действительной составляющей первого, чтобы получить реальную компоненту разности, и вычтите мнимую составляющую второго комплексного числа из мнимой составляющей первый должен прийти к мнимой составляющей разницы:
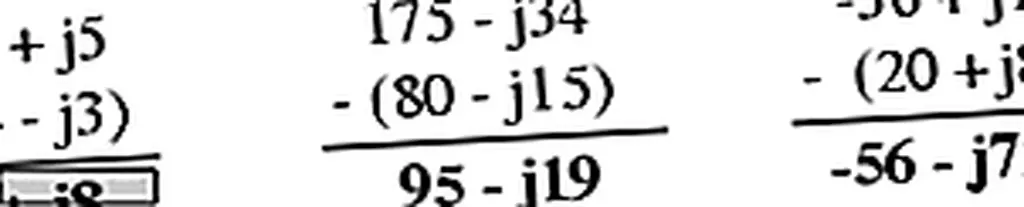
Для долговременного умножения и деления полярность - предпочтительная нотация для работы. При умножении комплексных чисел в полярной форме просто умножайте полярные величины комплексных чисел для определения полярной величины продукта и добавьте углы комплексных чисел для определения угла произведения:
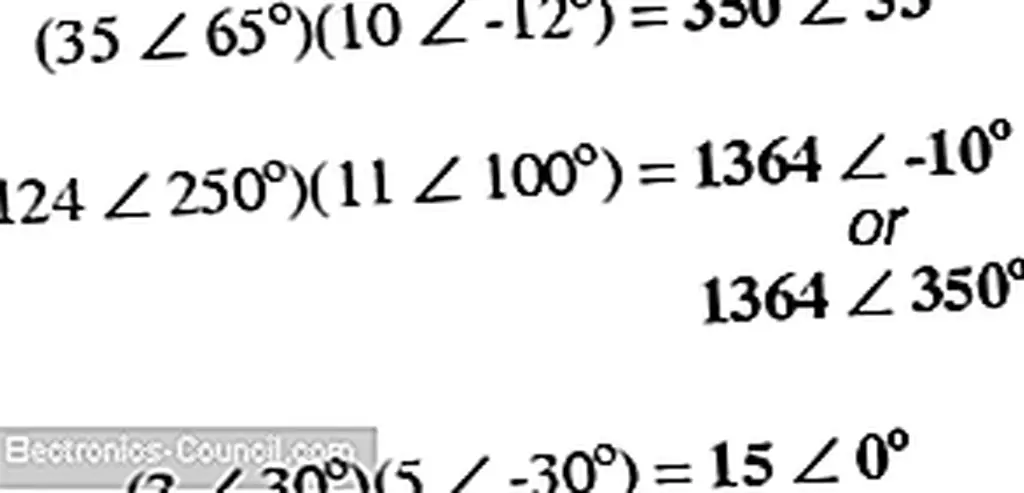
Разделение полных комплексных чисел также легко: просто разделите полярную величину первого комплексного числа на полярную величину второго комплексного числа, чтобы достигнуть полярной величины частного, и вычтем угол второго комплексного числа из угол первого комплексного числа достигнет угла частного:
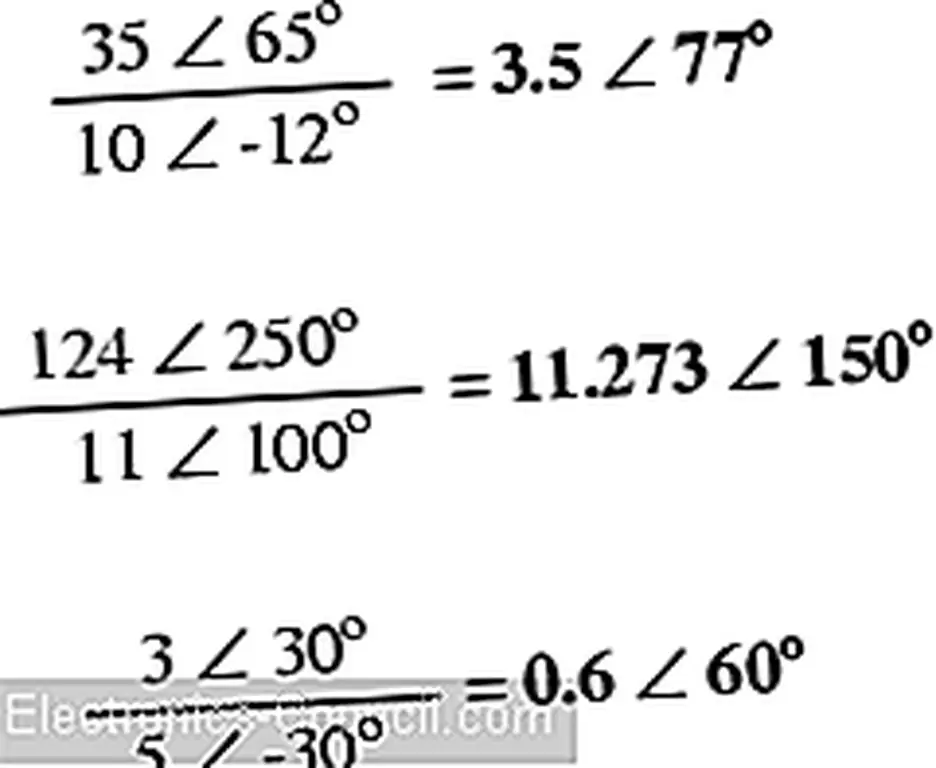
Чтобы получить обратное или «инвертированное» (1 / x) комплексное число, просто разделите число (в полярной форме) на скалярное значение 1, которое представляет собой не что иное, как комплексное число без мнимой составляющей (угол = 0):
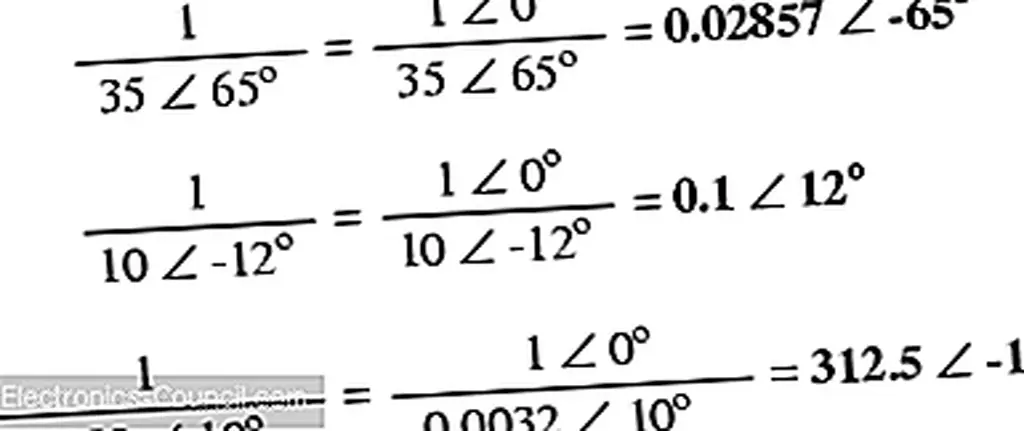
Это основные операции, которые вам понадобятся для управления сложными числами при анализе цепей переменного тока. Однако операции с комплексными числами никоим образом не ограничиваются только добавлением, вычитанием, умножением, делением и инверсией. Практически любая арифметическая операция, которая может быть выполнена со скалярными числами, может быть выполнена с комплексными числами, включая мощности, корни, решения одновременных уравнений с комплексными коэффициентами и даже тригонометрическими функциями (хотя это включает совершенно новую перспективу в тригонометрии, называемую гиперболическими функциями, которая хорошо выходит за рамки этого обсуждения). Убедитесь, что вы знакомы с основными арифметическими операциями сложения, вычитания, умножения, деления и инверсии, и у вас мало проблем с анализом цепи переменного тока.
- ОБЗОР:
- Чтобы добавить комплексные числа в прямоугольной форме, добавьте реальные компоненты и добавьте мнимые компоненты. Вычитание аналогично.
- Чтобы умножить комплексные числа в полярной форме, умножьте величины и добавьте углы. Чтобы разделить, разделите величины и вычтите один угол от другого.