Секи Кова (1642-1708): мудрец-арифметик
До Лейбница и Бернулли он открыл существенное содержание их математических работ.

Seki Kowa (также известный как Seki Takakazu) родился в драматический период японской истории: в середине 16-го века страна все еще была вовлечена в борьбу за власть между соперничающими принцами, которые пытались использовать сила, чтобы завоевать, чтобы получить суверенитет над страной (сёгунат). Наконец, решающую роль в войне сыграло огнестрельное оружие, завезенное в Японию европейскими торговцами. С 1543 года начали торговать купцы из Португалии, а затем и из других стран. За купцами последовали миссионеры, которые обратили в христианство сотни тысяч человек. Среди миссионеров были и иезуиты, которые информировали японских ученых о состоянии развития математики в Европе.
Европейские купцы и миссионеры пытались оказать политическое влияние. Затем, в 1598 году, Токугава Иэясу, одному из военачальников, удалось победить всех соперников и таким образом силой объединить Японию. Чтобы уменьшить возможное влияние Императора (Тэнно), он перенес резиденцию правительства из Киото в свою предыдущую штаб-квартиру, небольшую рыбацкую деревню под названием Эдо, которая позже получила название Токио (буквально: Восточная столица). Он изгнал из страны иностранных купцов и миссионеров, запретил христианскую веру и уничтожил христианские церкви. Лишь немногим голландским купцам, отвергавшим всякую мысль о прозелитизме, было позволено продолжать свою торговлю - для них был создан искусственный, обнесенный стеной остров в порту Нагасаки; торговому кораблю разрешалось заходить сюда только раз в год. На протяжении более 200 лет это была единственная связь Японии с внешним миром, поскольку правители также запрещали японским кораблям плавать в другие страны. Лишь в 1854 г. американские военные корабли насильственно нарушили одностороннюю изоляцию. Во время долгой фазы изоляции Япония пережила культурный ренессанс; Развивалась живопись и садовая архитектура, зародилась знаменитая чайная церемония, особый способ расположения цветов (икэбана). Математика тоже процветала.
Сэки Кова считается важнейшим представителем васан, японской математики эпохи Эдо - на его надгробии он упоминается как "арифметический мудрец". Он родился в конце 1642 года (за несколько месяцев до Исаака Ньютона), вторым сыном воина-самурая; в детстве он был усыновлен дворянской семьей. Уже в ранние годы узнаешь его особый математический талант; он помогает своему приемному отцу в учете и проверке налоговых сборов округа. Поскольку он проявляет особый интерес к математическим вопросам, он создает свою собственную библиотеку с книгами по математике на японском и китайском языках и интенсивно занимается их содержанием.
Две книги китайского математика Чжу Шицзе (1260-1330) оказали особое влияние на Секи Кова: «Введение в изучение математики» и «Драгоценное зеркало четырех элементов». В них, помимо прочего, составляются и решаются численно нелинейные уравнения с числом переменных до четырех (Чжу Шицзе называет это «методом небесных элементов»). Для определения решения уравнений высших степеней используется метод, очень похожий на метод Хорнера (названный в честь Уильяма Джорджа Хорнера (1786-1837)), который был разработан лишь 500 лет спустя в Европе.
Книга «Дзинко-ки» (Трактат о числах) Мицуёси (1598-1672) 1627 г. содержит, среди прочего, подходы к интегральному исчислению. Однако эта книга создает и новую традицию: даются дополнительные задачи, решение которых автор дать не может. Формулировка нерешенных проблем позже создает конкуренцию между школой Секи и (университетскими) школами Киото и Осаки.
Китайские книги по математике прибыли в Японию в 15 веке; книги сначала переиздаются без изменений, затем комментируются, а затем дополняются собственными мыслями редакции. Эти книги содержат задачи из различных областей математики в виде сборников упражнений с решениями; авторы объясняют методы решения с широким кругом тем, но не создавая «теоретической надстройки».
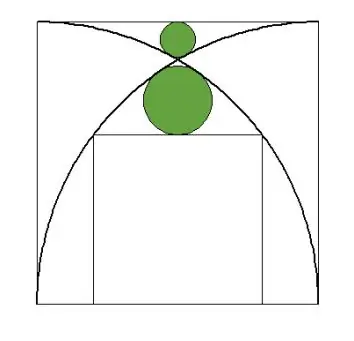
Книги, обучающие использованию японских счетов (соробан), также появляются. Характерны также для периода васан математические таблицы «храмовой геометрии» (сангаку), на которых отмечены геометрические задачи с вписанными или описанными окружностями, эллипсами, квадратами, ромбами и треугольниками; есть и пространственные проблемы. Эти искусно сделанные таблички вешают в буддийских храмах или синтоистских святилищах в качестве подношений - благодаря богам за просвещение в обнаружении и решении этой проблемы; они служат интеллектуальным вызовом для посетителей.
1670 в Осаке издана книга Савагути Казуюки, в которой среди прочего рассматриваются 150 проблем, для которых Мицуёси не смог дать решения. Ему удается решить 135 из 150 задач; остальные 15 проблем он описывает как «фактически неразрешимые».
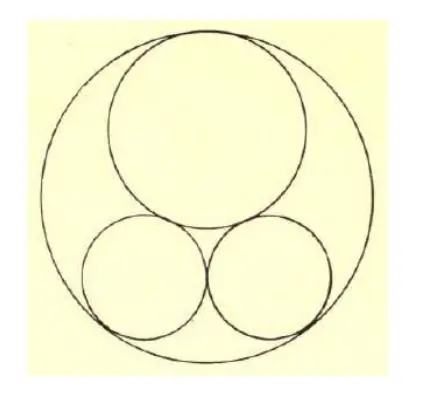
Одна из «неразрешимых» задач: «В окружность вписаны три другие окружности; оставшаяся площадь имеет 120 единиц площади. Общий диаметр двух малых окружностей на 5 единиц длины меньше диаметра окружности. третий круг. Каков диаметр кругов на рисунке?"
Сэки Кова прославился не в последнюю очередь благодаря книге «Хацуби Сампо», которую он опубликовал четыре года спустя; он содержит, среди прочего, решения всех 15 задач. В книге он представляет алгебраические термины в новых, изобретенных им самим обозначениях степеней. В своих решениях Секи старается, как это принято и в Европе, скрывать от конкурентов фактические методы решения (или даже способы их нахождения). Важно только то, что вы можете решить проблему самостоятельно разработанным, новым методом, а не почему этот метод подходит для решения проблемы. Решения, которые он на самом деле преследовал, стали известны только спустя десятилетия после его смерти.
В научной литературе Секи часто сравнивают с Ньютоном с точки зрения его значения. Методы, разработанные им (возможно, также его учеником Катахиро Такебе), выходят далеко за рамки того, что можно найти у Чжу Шицзе: его книги содержат обобщенные схемы (численного) решения любых алгебраических уравнений. Для решения систем линейных уравнений с тремя переменными он использовал метод, с помощью которого решения получали из таблиц с коэффициентами уравнений, - сравнимый с методом определителя, открытым Готфридом Вильгельмом Лейбницем (1646-1716) десятью годами позже; Секи также показывает законы перестановок, применимые к детерминантам. Он дает формулы для суммы первых k степеней натуральных чисел - таким образом находит числа Бернулли до Якоба Бернулли (1655-1705).
Сэки и Такебе вычисляют количество окружностей по методу Энри (принцип окружности), своеобразной, необычной процедуре: учитываются бесконечно малые дуговые сегменты по хордам, которые рассчитываются шаг за шагом с возрастающей точностью - определение производится с точностью до десяти знаков серийной разверткой (!).
Наконец, в книгах Секи вы также найдете множество упражнений по занимательной математике, например, способы построения магических квадратов или магических кругов. Только в 1868 году книги васан в Японии были заменены книгами в западном стиле, то есть со схемой доказательства теоремы определения, которая использовалась со времен Евклида.
