Как узнать, было ли захвачено или убито достаточное количество членов террористической ячейки, чтобы с высокой вероятностью эта ячейка больше не могла осуществлять атаку? Математическая модель террористических организаций может дать некоторые подсказки. Вопрос в том, какая математическая модель будет работать лучше всего.
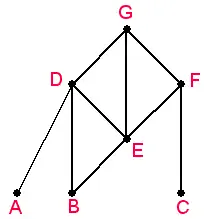
Один из способов описания террористической организации - это граф - паутина линий, соединяющих узлы. В этой модели каждый узел будет представлять отдельного члена данной ячейки, а линия, соединяющая два узла, будет указывать на прямую связь между этими двумя членами.
Когда член ячейки захвачен или убит, соответствующий узел удаляется из графа. Влияние таких потерь на эффективность ячейки можно оценить, рассмотрев, как затронуты связи между членами ячейки. Удаление достаточного количества узлов приводит к нарушению работы.
Математически вы могли бы задать вопрос: сколько узлов вы должны удалить из данного графа, прежде чем он разделится на две или более отдельных частей?
Для графов различных типов можно оценить вероятность того, что удаление определенного количества узлов разделит граф на две или более отдельных единиц.
Графовая модель, возможно, не самая лучшая из доступных для представления типичной террористической организации, утверждает математик Джонатан Д. Фарли из Массачусетского технологического института. Он специализируется на теории решеток и теории упорядоченных множеств.
«Мы считаем, что моделирование террористических сетей в виде графов не дает нам достаточно информации для борьбы с угрозой», - написал Фарли в недавнем выпуске «Исследований конфликтов и терроризма». «Моделирование террористических ячеек в виде графов игнорирует важный аспект их структуры, а именно их иерархию и тот факт, что они состоят из лидеров и последователей.”
Недостаточно отключить террористические сети, утверждает Фарли. Остаток все еще может содержать лидера и достаточно последователей, чтобы организовать серьезную атаку.
Фарли предложил альтернативный подход, который лучше отражает иерархию организации. «Мой метод использует теорию порядка для количественной оценки степени, в которой террористическая сеть все еще способна функционировать», - говорит он.
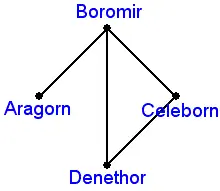
В этом случае становится важным отношение одного человека к другому в ячейке. Лидеры представлены самыми верхними узлами на диаграмме упорядоченного набора, представляющего ячейку, а пехотинцы - узлами внизу. Разрушение организации было бы равносильно нарушению цепочки подчинения, что позволяет приказам передаваться от лидеров пехотинцам.
Цепочка команд, связывающая лидера с пехотинцем, называется максимальной цепью в упорядоченном множестве. В заданном упорядоченном множестве таких цепей может быть несколько. Все эти цепочки должны быть разорваны, чтобы ячейка (или остаток) считалась неэффективной.
Анализ структуры и общих узлов таких цепочек позволяет определить вероятность разрушения террористической ячейки. Фарли разработал формулу для этого расчета.
Вообще, формула Фарли дает более низкие вероятности успеха, чем те, которые дает простая графовая модель.
Фарли предполагает, что его метод анализа может помочь чиновникам принимать решения о распределении ресурсов, денег и персонала для борьбы с терроризмом. «Этот инструмент поможет правоохранительным органам узнать, когда битва с «Аль-Каидой» выиграна, тем самым сэкономив деньги общества без чрезмерного риска для его безопасности», - говорит он.
В то же время Фарли признает, что его модель «разорвать цепи» можно было бы улучшить. Его можно модифицировать, например, для отражения более сложных иерархий, зависимости от ранга вероятности быть захваченным, влияния течения времени и других факторов.
Модель Фарли имеет несколько недостатков. Правоохранительные органы часто не знают, как организована террористическая ячейка или даже ее полный состав. Также неясно, происходят ли теракты именно тогда, когда приказы от лидеров передаются пехотинцам.
Тем не менее, утверждает Фарли, «эта модель позволяет правоохранительным органам планировать свои операции менее спонтанно, чем они могли бы делать в противном случае».