Запрещенные простые числа
Числа - это не просто числа. Они могут быть веселыми, счастливыми или сексуальными. А иногда они даже незаконны.

Нетрудно еженедельно заполнять эту колонку статьями о простых числах. Они занимали математиков с древности до наших дней. Они являются атомами мира чисел и влияют на все дисциплины математики. Вы уже знаете, что такое простое число в школе: целое, положительное число (больше единицы), которое можно разделить только на единицу и на себя без остатка. Но что вы обычно не изучаете, так это множество специальных типов простых чисел, которые математики определили с течением времени.
Например, простые числа Жермена, названные в честь Софи Жермен: число p является простым числом Жермена тогда и только тогда, когда число 2p+1 также является простым числом. Например, 11 удовлетворяет условию, так как 211+1=23 также является простым числом. Известно 190 простых чисел Жермена от 1 до 10 000; сколько их всего и бесконечно ли много - как и в случае с обычными простыми числами - до сих пор никто не знает.
Концепция простых чисел Мерсенна важна при поиске особенно больших простых чисел (например, используемых для методов шифрования). Так называются простые числа, которые можно записать в виде 2^n-1. Многие другие простые числа были названы в честь других математиков, но есть также «слабые простые числа», «счастливые простые числа», «счастливые простые числа» и даже «сексуальные простые числа». Последние представляют собой пары простых чисел, разность которых равна ровно 6, например 5 и 11, 7 и 13 или 11 и 17.
Если вы зайдете достаточно далеко в мир особых (и странных) простых чисел, вы сможете сделать много удивительных открытий. Например, с помощью этой формулы, описывающей простые числа Вильсона:
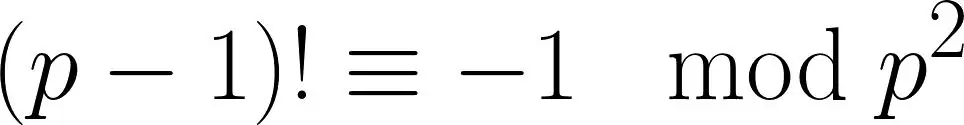
Это означает не что иное, как: Простое число p является простым числом Вильсона, если (p-1)!+1 без остатка делится на p². Число 5 показывает, как работает принцип. 5-1 равно 4.! является символом необязательного умножения и означает здесь, что мы должны умножить числа от 1 до 4 вместе: 4!=1234=24. Теперь прибавляем 1 и получаем 25. И это делится нацело на 5²=25. Итак, 5 - простое число Вильсона. Принцип выглядит простым и легко применимым. Несмотря на это, на сегодняшний день известны только два других простых числа Вильсона (13 и 563). Если простых чисел Вильсона больше, то они определенно больше 500 миллионов. Почему эти числа ведут себя так странно, неизвестно.
Так называемые «незаконные простые числа» немного страннее. Они больше не определяются чистой математикой, а связаны с программированием компьютеров и правовой системой. Говорят, что простое число недопустимо, если содержащаяся в нем числовая информация где-то недопустима. Например, в 2001 году программист Фил Кармоди обнаружил 1401-значное простое число, идентичное сжатому исходному коду программы DeCSS. С помощью этой программы вы можете расшифровать зашифрованное содержимое на DVD, поэтому распространение этой программы запрещено во многих странах. Теоретически, после открытия Кармоди, распространение простого числа теперь также должно было быть запрещено, но это было бы трудно оправдать.
Поиск «нелегального» номера был частью акции протеста против судебного преследования авторов DeCSS. Они хотели найти способ распространения программы, против которого не могли бы возразить судебные органы.
Вы можете думать об этой цели, что хотите. Однако открытие незаконного простого числа ясно показывает, что от силы чисел и формул просто не убежать. Числа несут информацию, а любую информацию можно описать числами. Математика часто может казаться абстрактной. По правде говоря, она везде.
