Все изменения стоят на месте…
… если этого требует теорема о неподвижной точке. Иногда математика становится по-настоящему увлекательной только тогда, когда больше ничего не происходит. Вы можете рассчитать, когда это так.

В математической формуле вы вводите числа или символы на одном конце, а другие числа или символы появляются на другом конце. Как бы банально это ни звучало, это почти всегда правильно. Но только почти: иногда ввод и вывод идентичны, и именно тогда во многих случаях становится особенно интересно. Потому что тогда вы нашли так называемую фиксированную точку:
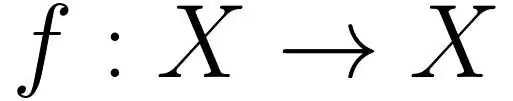
Это простое уравнение описывает отображение f, отображающее множество X на себя. Или, говоря проще: если у вас есть математическая функция f, то число является фиксированной точкой тогда и только тогда, когда f(x)=x. Такие точки не всегда должны существовать. Например, если задана функция f(x)=x ² - 5 x + 9, довольно быстро становится ясно, что x=3 должна быть фиксированной точкой. Столь же быстро становится ясно, что функция f(x)=x + 3 заведомо не может иметь неподвижной точки. Однако в более сложных задачах на первый взгляд не очевидно, есть ли у отображения неподвижные точки или нет. Для этих случаев в математике имеется большой набор так называемых теорем о неподвижных точках, которые точно сообщают вам, при каких условиях существуют или не существуют фиксированные точки.
Фиксированные точки имеют большое значение практически во всех областях математики. Впервые я столкнулся с ними, когда изучал движение астероидов и планет в своей работе небесного механика. Соответствующие уравнения описывают, как изменяются положение и скорость исследуемого небесного тела. Вы выбираете начальное состояние, и уравнения движения говорят мне, каким будет состояние объекта в более поздний момент времени. Однако, если это состояние больше не меняется, т.е. всегда остается одним и тем же от временного шага к временному шагу, то вы нашли фиксированную точку. Например, устойчивая орбита или точка равновесия динамической системы.
Эти точки баланса важны и в других дисциплинах. Математик Джон Нэш создал центральную концепцию теории игр, назвав в его честь «равновесие Нэша». Речь идет о математическом анализе решений игроков в играх, что, безусловно, может описать реальные сценарии конфликта или сотрудничества. Однако в целом вы не знаете, как решат другие игроки или как ваше собственное решение повлияет на действия других игроков. В своем анализе Нэш предположил все возможные стратегии всех игроков, а затем определил те, в которых ни у одного отдельного игрока не было стимула отклоняться от своей соответствующей стратегии. Другими словами, в равновесии по Нэшу каждый игрок думает, что сделал все возможное в данных обстоятельствах, и понимает, что любой другой вариант приведет к худшему для него результату.
Ничего не работает (лучше)
Равновесие Нэша, таким образом, представляет собой фиксированную точку теоретико-игровых алгоритмов, и поиск таких фиксированных точек является важным экономическим приложением математики. Любой может легко опробовать на себе концепцию фиксированных точек. Для этого вам понадобится калькулятор, который может вычислить косинус любого действительного числа (убедитесь, что вы делаете расчет в режиме «радианы»). Результат служит входными данными для нового вычисления косинуса и так далее. Независимо от того, с какого числа вы начнете: в конце результат всегда будет ближе к числу 0, 739085133… Потому что это в точности фиксированная точка уравнения f(x)=cos(x) или, если рассматривать графически, пересечение функции косинуса и диагонали y=x в системе координат.
Математика - прекрасный инструмент для описания, расчета и прогнозирования изменений. Но иногда вам также нужно знать, когда что-то не изменится. Если все остается так, как есть, это зачастую интереснее, чем постоянное изменение. Теоремы о неподвижной точке различных математических дисциплин говорят нам, при каких обстоятельствах изменение прекращается, и именно поэтому они так важны.
