Сила чисел
Некоторые формулы кажутся настолько абстрактными, что почти бесполезны. Но сила в числах - и им требуется совсем немного времени, чтобы раскрыть свои секреты.

В 1831 году математик Август Фердинанд Мёбиус ввел в математику новую функцию:
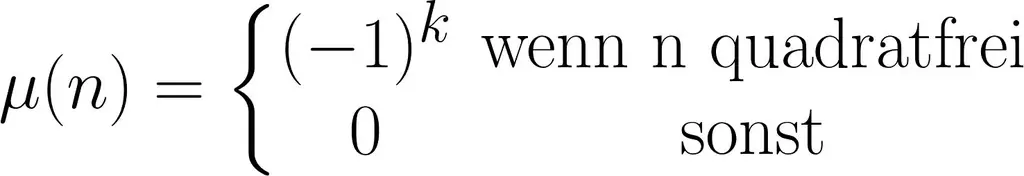
Эта функция Мебиуса, которая сегодня носит его имя, не сложна, но требует небольшого пояснения. Функция может иметь только три различных значения: -1, 0 и +1. В функции можно использовать любое натуральное число больше нуля. Он принимает значение 0 для всех чисел, являющихся квадратом натурального числа или кратным ему (например, 4, 8, 9, 12, 16, 18, …). Для других, бесквадратных чисел, есть две возможности. Если число имеет нечетное количество простых множителей (обозначается k в формуле), то значение функции равно -1; четное число простых множителей дает +1.
Вот вам и определение. Но зачем вам это нужно? Этот вопрос неуместен в математике (и, по-моему, и в других естественных науках). Функцию можно определить, и если ее можно определить, то она существует в математическом мире. Его можно исследовать, и результат этого анализа создает дополнительные математические знания.
Наконец, функция Мебиуса также имеет свое применение. Оно возникает, например, при изучении знаменитой функции Римана, лежащей в основе одной из величайших нерешенных проблем математики. Это связано с теоремой о простых числах, одним из самых важных утверждений в теории чисел. И неожиданно всплывает странная черта 19-го века. Века также с одной из больших физических проблем настоящего.
В 1989 году физик Бернхард Юлия разработал идею «примонового газа». Это пример модели, которая создает связь между квантовой теорией поля и теорией чисел. Гипотетические частицы, описанные в этой модели, называются «примонами». У них есть энергии, которые определяются простыми числами. Первоначальный примонный газ имеет дело с бозонами, то есть с теми элементарными частицами, которые отвечают за посредничество сил в стандартной модели физики элементарных частиц. К ним относятся, например, фотоны или глюоны. Однако в контексте того, что известно как «суперсимметрия», физики уже какое-то время пытаются расширить классическую модель, среди прочего, для того, чтобы включить гравитационную силу в квантово-механические описания или иметь возможность объяснить Природа темной материи. Для этого устанавливается связь между бозонами и фермионами, т. е. между элементарными частицами, из которых состоит материя (электроны, кварки и т. д.). Каждой частице силы соответствует частица материи и наоборот.
Если переформулировать модель примонного газа так, чтобы она обладала еще и суперсимметричными свойствами, то в математическом анализе вы столкнетесь с функцией Мёбиуса. Значение, которое оно принимает, больше не зависит от свойств натуральных чисел, а меняется в зависимости от того, описывается ли оно бозоном или фермионом. Он становится равным нулю при работе с квантово-механическими состояниями, исключаемыми принципом Паули (который утверждает, что два фермиона не могут находиться в одном и том же состоянии).
Конечно, примонный газ - это всего лишь модель в качестве примера, предназначенная для лучшего понимания некоторых свойств частиц, а не реальная попытка описать природу. И предсказания суперсимметрии не могут быть экспериментально подтверждены до сих пор, несмотря на многочисленные усилия.
Тем не менее: Август Фердинанд Мёбиус, вероятно, был бы очень удивлен, если бы узнал, что его странная функция над натуральными числами используется сегодня для описания фундаментальных строительных блоков мира.
