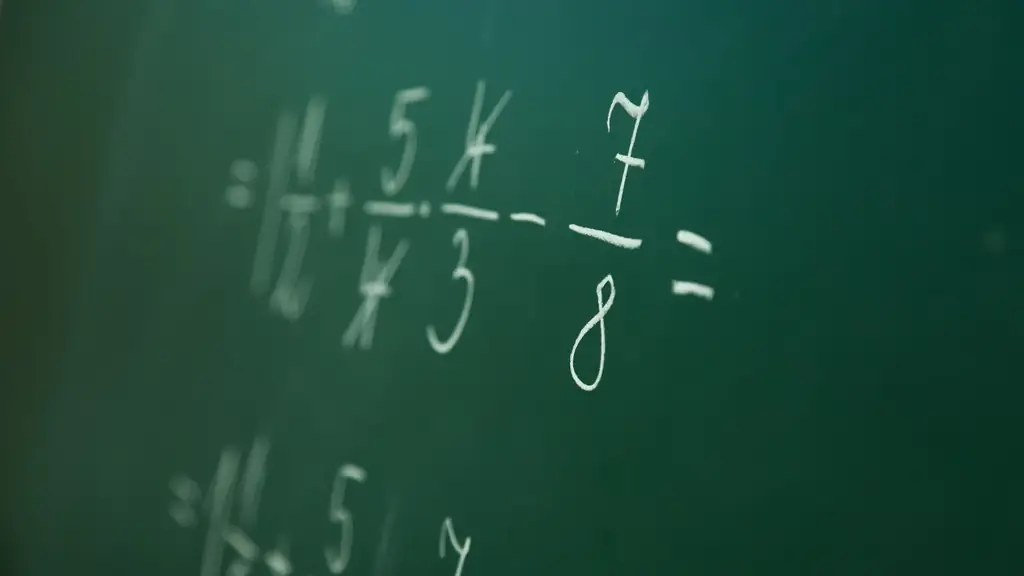Неожиданный взрыв номеров
Последовательность Фарея - это результат обдумывания ошибки новичка до конца. Вы можете поиграть с ней в милые игры или решить один из самых сложных вопросов по математике.
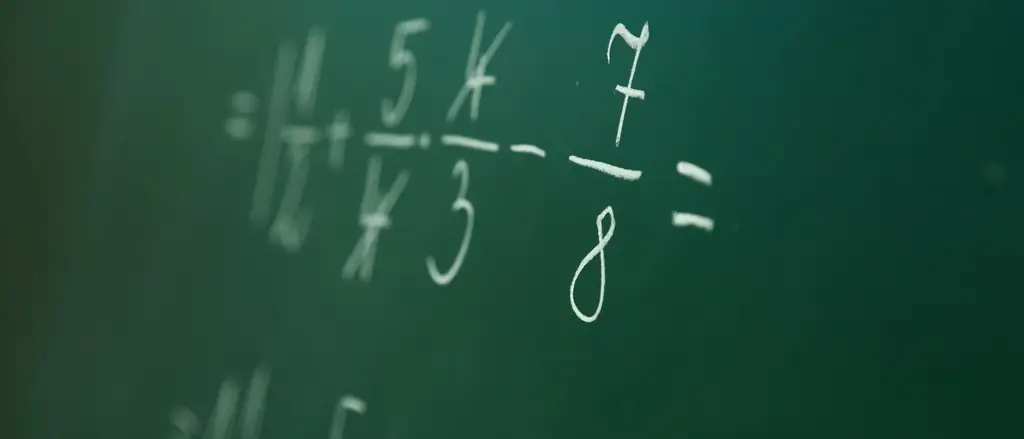
Это может немного сбить с толку, когда вы впервые сталкиваетесь с числами, которые не являются сами по себе, а расположены по обе стороны от дроби. Особенно, когда речь идет о проведении с ним обычных арифметических действий. Давайте посмотрим на эту формулу:
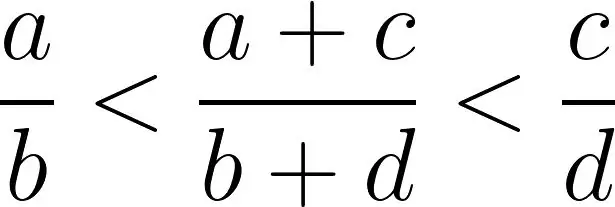
В середине этого неравенства стоит математическое выражение, которое, вероятно, зачеркнуто красным в тетрадях многих школьников. Если вы хотите сложить дроби a / b и c / d, то заманчиво просто записать результат как (a + c) / (b + d). Это неверно, хотя это выражение имеет определенное значение в математике. Он называется «медианой» двух исходных дробей, потому что его значение всегда находится между двумя исходными числами.
Самые легендарные математические приемы, самые страшные камни преткновения в истории физики и всевозможные формулы, в которых едва ли кто-то может увидеть дремлющий в них смысл: Это обитатели мира формул Фрейстеттера.
Вы можете найти все выпуски его еженедельной колонки, которая выходит каждое воскресенье, здесь.
Например, если вы запишете первую дробь как 4/5, а вторую как 6/7, то медиана составит 10/12 (=5/6) между ними. Не обязательно ровно посередине - но неравенство по-прежнему применяется в любом случае при условии, что b и d больше нуля, а a/b меньше c/d.
Французскому математику Николя Шюке, как говорят, удалось открыть это так называемое «правило средних чисел» еще в 15 веке. И даже если это звучит немного тривиально, в этом есть нечто большее, чем кажется на первый взгляд. Если вы начнете с двух дробей 0 / 1 и 1 / 1, то логически вы получите медиану 1 / 2. Теперь вы можете вычислить две медианы между этими тремя дробями и получить результат: 0 / 1 … 1 / 3 … 1/2…2/3…1/1. Продолжая схему, получаем 0/1…1/4…1/3…1/2…2/3…3/4…1/1.
Эпизод с любопытными свойствами
Любой, кто занимался теорией чисел немного более интенсивно, узнает в этих дробях так называемую "последовательность Фарея". Последовательность Фари n-го порядка получается путем записи по порядку максимально сокращенных дробей от 0 до 1, чей знаменатель не превосходит n. Таким образом, приведенные выше примерные расчеты в результате дали последовательности Фарея порядков 1, 2 и 3. Свое название они получили от английского геолога Джона Фари, который, глядя на таблицу с приведенными дробями, заметил связь с медиантами.
1816 г. он написал письмо в «Философский журнал» («О любопытном свойстве вульгарных дробей») и спросил, известно ли уже или доказано это свойство. Удивительно, но такого доказательства все еще не было, но оно было быстро предоставлено известным математиком Огюстеном-Луи Коши после прочтения заметки Фарея. Связь между медиантами и редуцированными дробями ранее была открыта математиком Чарльзом Харосом, но ни Фейри, ни Коши не знали об этом.
Вы можете делать интересные вещи с последовательностями Farey. Если вы создадите диаграмму, в которой соответствующие знаменатели дроби последовательности отмечены на оси x, а числители отмечены на оси y, и соедините полученные точки линией, вы получите очень характерный зигзагообразный узор.. Отражение его относительно главных осей и диагонали дает кривую, напоминающую то, как взрыв изображается в комиксе.
В дополнение к этому чисто визуальному аспекту, возможно, можно также найти доказательство гипотезы Римана в последовательности Фарея. Это одна из самых важных нерешенных математических задач, в которой содержатся утверждения о распределении простых чисел. С 1859 года она не была ни доказана, ни опровергнута. Но в 1924 г. удалось показать, что оно эквивалентно утверждению о расстояниях членов в последовательностях Фарея. Это утверждение также бездоказательно. Но, возможно, именно дроби в конце концов приведут к успеху.