Математика без права на существование?
Иногда математика похожа на искусство. Для некоторых формул не требуется собственного обоснования. Твоего увлечения достаточно. А иногда польза приходит позже.
Легендарный индийский математик Шриниваса Рамануджан был известен своим неортодоксальным подходом к работе и своими формулами, которые - по крайней мере, в глазах коллег - он вывел совершенно неожиданно, из ниоткуда. Одно из самых удивительных уравнений, с моей точки зрения, это:
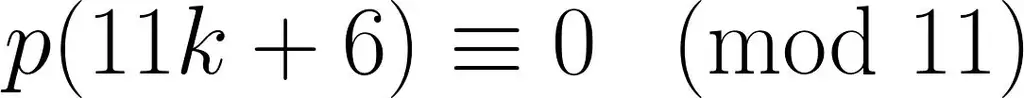
На самом деле она выглядит безобидной, но внешность обманчива. Функция p обозначает функцию статистической суммы и дает количество способов разложить положительные целые числа на положительные целые слагаемые.
Например, число 4 можно записать как 1+1+1+1, 1+1+2, 2+2, 1+3 или просто 4. Это пять возможностей, поэтому p(4)=5. Есть семь способов разделить 5, 30 способов разделить 9 и целых 190 569 292 способа сложить 100.
В начале 20 века математики пытались найти общую формулу для расчета количества возможных разделов для любого заданного числа. До этого единственным способом вычислить статистическую сумму было более или менее попытаться подсчитать различные варианты. Это все еще было возможно с небольшими числами, но очень быстро стало очень громоздким с большими числами.
Рамануджан также изучал эту проблему и столкнулся с тем, что теперь известно как «соответствия Рамануджана». Один из них описывается приведенной выше формулой: если число ровно на 6 больше, чем число, кратное 11, то значение соответствующей статистической суммы также кратно 11. Другими словами, если вы подсчитаете количество разделов для 6, 17, 28, 39, 50, 61 и т. д., результат всегда делится на 11 без остатка.
Ввиду таких заявлений вполне понятно, что коллеги Рамануджана утверждают, что все положительные целые числа являются его «личными друзьями». Вместе с британским математиком Годфри Гарольдом Харди Рамануджану сначала удалось найти приблизительную формулу для оценки статистической суммы, а позже даже формулу для прямого вычисления возможных разбиений..
Для меня такая высокотворческая и интуитивная математика самодостаточна. Подобно искусству, оно на самом деле не нуждается ни в каком дальнейшем оправдании; обаяния, присущего таким формулам, абсолютно достаточно как raison d'être. Такого же мнения был и коллега и друг Рамануджана Харди, отвергавший - особенно военные - приложения математики и написавший в своих мемуарах: «Я никогда не делал ничего «полезного». Ни одно из моих открытий никогда не приводило и, вероятно, никогда, прямо или косвенно, к добру или к худу, не повлияет на благосостояние мира».
Конечно, в этом он ошибался, потому что рано или поздно каждому математическому знанию найдется соответствующее применение. «Чистая» теория чисел, которую Харди практиковал вместе с Рамануджаном, сегодня составляет основу всех систем шифрования, с помощью которых мы работаем в Интернете и онлайн-торговле. И даже столь абстрактные разбиения нашли свое применение в информатике и технике. Например, когда речь идет о распределении вычислительных задач в многопроцессорных системах, чтобы каждый процессор выполнял примерно одинаковый объем работы, единственный способ сделать это - вычислить статистическую сумму. Когда современные ученые используют суперкомпьютеры для создания климатических моделей или имитации ядерных взрывов при разработке ядерного оружия, они делают это, в частности, на основе работ Харди и Рамануджана - и опровергают их так ясно, что их открытия не вносят никакого вклада в «добро или зло»...