Иногда достаточно сосчитать до двух
Математика не требует много времени, чтобы поднимать сложные вопросы. В некоторых ситуациях вам нужны только цифры 1 и 2. Например, в случае последовательности Колакоски.

Математика имеет большой запас символов для самовыражения. Это может сбивать с толку, если вы не знаете словарный запас. Но при небольшом творчестве достаточно двух чисел, чтобы удивить. Как в этой формуле:
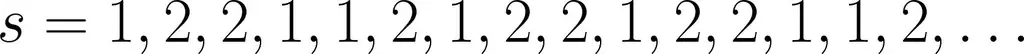
Если вы посмотрите на эту последовательность чисел, то сразу заметите, что это просто цифры 1 и 2. Также поразительно, что цифры появляются только поодиночке или парами. Чтобы увидеть, как возникает последовательность единиц и двоек, вам нужно подумать еще немного. В точном математическом выражении это последовательность длин серий, которая в то же время является кодированием длин серий. Короче говоря, если мы посчитаем, сколько раз повторяется каждая цифра, и запишем результат, то полученная последовательность будет идентична последовательности, элементы которой мы подсчитали.
Первый блок состоит из одной цифры 1, поэтому его длина серии равна 1. Второй блок - повторение цифры 2 - имеет длину серии 2. Затем идет блок с двумя единицами, так что один тоже ствол длиной 2. Далее следует одна двойка, т. е. блок с длиной серии 1 и так далее. Если мы запишем последовательность длин серий, определенных до сих пор, результатом будет 1, 2, 2, 1. Это точно соответствует началу исходной последовательности. Можно легко убедиться, что оценка длин серий действительно воспроизводит полную последовательность.
Также можно построить последовательность непосредственно из себя. Для этого задаются первые три значения последовательности: 1, 2, 2. Последние 2 в этой стартовой последовательности означают, что теперь должен следовать блок с длиной прогона 2; так что это должно продолжаться с 1, 1. Эти два новых числа в последовательности, в свою очередь, определяют, что теперь должно быть два блока с длиной цикла 1 каждый. Таким образом, вы добавляете 2 и 1 к последовательности, в результате чего получается 1, 2, 2, 1, 1, 2, 1. Затем должен быть блок с длиной серии 2, за которым следует блок с длиной серии 1: 1, 2, 2, 1, 1, 2, 1, 2, 2, 1. Это можно продолжать до бесконечности.
Периодична ли последовательность Колакоски?
Легко запутаться во всех единицах и двойках, но на самом деле легко записать странную последовательность. Американский математик Руфус Ольденбургер впервые сделал это в 1939 году, хотя и в очень специфическом контексте символической динамики, который вряд ли привлек бы внимание большого числа математиков. Напротив, художник Уильям Колакоски преуспел. Хотя он очень интересовался математикой и философией, предпочитал изучать искусство. Тем не менее в 1965 г. он отправил короткую заметку в The American Mathematical Monthly. В нем он указывал на существование числового ряда единиц и двоек, который он открыл независимо от Ольденбургера, и просил дать простой метод, чтобы можно было описать, как можно вычислить эту последовательность и является ли она периодической, т. е. со временем начинают повторяться.
Самые легендарные математические приемы, самые страшные камни преткновения в истории физики и всевозможные формулы, в которых едва ли кто-то может увидеть дремлющий в них смысл: Это обитатели мира формул Фрейстеттера.
Вы можете найти все выпуски его еженедельной колонки, которая выходит каждое воскресенье, здесь.
Является ли последовательность Колакоски, как ее теперь обычно называют, действительно периодической или не показывает закономерностей, до сих пор неизвестно. Также неизвестно, есть ли в предельном случае бесконечно длинной последовательности больше единиц или двоек, или и то, и другое присутствует одинаково часто.
Сам Колакоски ценил этот эпизод в первую очередь за его эстетический и философский подтекст. Пожизненный шизофреник, он увидел странный хаотический порядок в последовательности: правила, которые их порождают, не поддаются интерпретации, однако последовательность чисел ведет себя непредсказуемым образом.
