Бесконечное количество пива после работы
Математики - бережливые люди: даже если бесчисленное количество их ходит в паб, они не пропивают припасы.

Бесконечное количество математиков ходит в бар. Первый заказывает пиво. Второй заказывает полпива. Третий четверть пива. Четвертый восьмую часть пива. беспокой меня, - говорит бармен и ставит на прилавок две банки пива».
Я разместил эту шутку в начале 2018 года в Твиттер-аккаунте «Разрушителей науки», группы научного кабаре, к ансамблю которой я принадлежу. И даже больше года спустя он все еще занимает последователей. Очевидное противоречие в шутке одновременно сбивает с толку и интригует. «Два пива никогда в жизни не хватит на БЕСКОНЕЧНОЕ количество математиков», - сказал один из последователей, и даже долгая дискуссия не смогла убедить его в обратном.
Задействованная математика не является тривиальной, но при ближайшем рассмотрении она не слишком сложна. Это геометрический ряд:
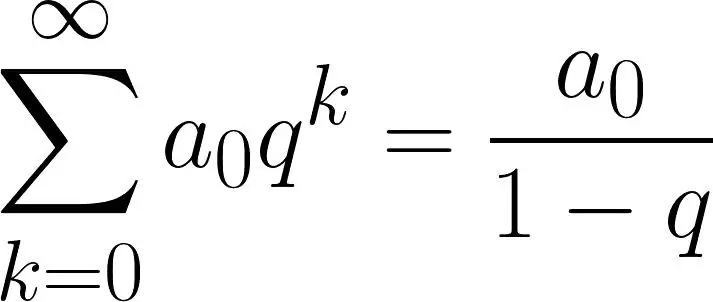
Эта формула применяется, если частное q не больше 1 и не меньше -1. При начальном значении a0=1 и q=½ последовательность из шутки получается точно. Вы ставите 0, 1, 2, 3, … в формулу друг за другом и складываете результаты: 1+ ½ + ¼ + ⅛ + … Бармен уже знает предельное значение последовательности, которое составляет рассчитывается по формуле, и знает, что он может обойтись двумя полными пивными стаканами и, следовательно, может обслужить бесконечное количество математиков. Чем больше становится k, тем меньше становится qk, и в целом общая сумма всех членов никогда не может быть больше 2.
Бесконечное количество пива после работы
Вы можете точно рассчитать это предельное значение, но вы также можете проиллюстрировать поведение ряда геометрически. Представим себе прямоугольник с длинами сторон 1 и 2, который, следовательно, имеет площадь 2, и вычеркнем прямоугольники, площадь которых соответствует членам ряда. Первый член ряда представляет собой квадрат со стороной 1 и площадью 1, т.е. ровно половину исходного прямоугольника. Для второго члена нам нужно удалить прямоугольник с площадью ½, то есть прямоугольник с длинами сторон 1 и ½, который теперь составляет ровно половину оставшегося квадрата.
Третий член - ¼ - теперь ровно половина оставшейся половины (квадрата со стороной 0,5). Из ½ квадрата, который у нас остался, четвертый член - ⅛ - снова занимает половину (прямоугольник со сторонами 0,5 и 0,25). И т.д. Каждый последующий термин вписывается в ту часть исходного прямоугольника, которая еще не была заявлена. В пределе бесконечного числа членов прямоугольник полностью заполняется и получается предел 2..
Геометрические ряды такого рода встречаются не только в научных анекдотах, но и во многих областях чистой и прикладной математики. Например, при расчете процентов или степенных рядов. Геометрический ряд также может быть использован для объяснения другого загадочного примера бесконечности: тот факт, что 0,99999… равно 1, Кажется, что никакое количество знаков после запятой не может составить 1 из числа, которое начинается с 0 перед запятой. Но эта десятичная дробь есть не что иное, как геометрический ряд с a0=9/10 и q=1/10, поэтому бесконечная сумма 0,9 + 0,09 + 0,009 +… Предел, рассчитанный из вышеприведенная формула равна 0,9, деленной на (1 - 0,1), и точно равна 1.
Бесконечность может сбивать с толку. У нас нет интуитивного понимания того, что происходит, когда мы имеем дело с поистине бесконечным процессом. Мы должны прибегнуть к математике и признать, что результаты противоречат нашему здравому смыслу. И эта бесконечность иногда имеет конец. В данном случае более двух пинтов пива - хотя некоторые могут захотеть и больше, чтобы сделать более сбивающие с толку аспекты бесконечности более терпимыми.
