Настоящих чисел недостаточно
Математическая уловка или реальность? Действительных чисел недостаточно для описания всех причудливых процессов квантовой механики. Также нужно воображаемое.

Одно только название показывает, что французский ученый Рене Декарт думал о корнях отрицательных чисел: «Мнимые числа» были столь же сложными, сколь и бесполезными, сказал его коллега Джироламо Кардано ранее в 16 веке, потому что никто не мог вообразите что-то внизу в это время. Теперь они прочно укоренились в математике и естественных науках, а некоторые даже знакомятся с ними в школе.
Потому что, вопреки мнению Кардано, комплексные числа, состоящие из действительных и мнимых чисел, оказываются чрезвычайно полезными. С его помощью гораздо легче выразить многие отношения, например, теорию электромагнетизма. Поэтому большинство профессионалов считают их полезным инструментом, упрощающим утомительные расчеты.
Однако квантовая механика выделяется на фоне других научных дисциплин: если вы хотите описать неинтуитивные процессы в микромире, без корней из отрицательных чисел обойтись сложно. Но обязательны ли комплексные числа для теории? Два эксперимента, результаты которых были опубликованы в декабре 2021 года, говорят именно об этом.
Вопреки всей интуиции
Процессы квантовой механики сильно отличаются от того, с чем люди сталкиваются в своей повседневной жизни: частицы не принимают фиксированное состояние, пока они не будут измерены, а могут быть описаны только как суперпозиция. Соответственно, электрон может находиться в двух и более местах одновременно. Если вы хотите предсказать результат измерения, который четко определяет состояние объекта, вы можете указать только вероятности, которые рассчитываются с помощью комплексных чисел.
Физиков-теоретиков, тем не менее, интересовало, возможно ли реальное описание в принципе. Для этого они сначала обратились к простым системам, состоящим из одной частицы. В таком случае можно найти математическую формулировку, основанную только на реальных значениях, но нужно вдвое больше измерений, чем в сложном варианте. В этом нет ничего удивительного: комплексное число z всегда можно представить в виде суммы z=a + i b, где a и b - вещественные числа, а i - квадратный корень из -1. В этом отношении z можно рассматривать как двумерный действительный вектор (a, b), который следует очень специфическим правилам расчета.
Таким образом, простые квантовые системы, состоящие из отдельных частиц, без проблем могут быть описаны вещественными числами. Однако, как только вы переходите к операциям с несколькими объектами, все становится сложнее. В дополнение к суперпозиции существуют и другие необычные квантово-механические явления, которые особенно очевидны в системах многих частиц. Сюда относится, например, запутанность: две или более частиц могут быть связаны друг с другом таким образом, что измерение одной напрямую влияет на состояние другой - независимо от того, насколько далеко они друг от друга. Чтобы представить эту сильную связь, нужна математическая операция, тензорное произведение. Аналогичную связь можно найти и для реального случая. Это позволяет описать любое количество запутанных частиц, исходящих из одного источника и измеряемых независимо друг от друга.
Эксперимент должен прояснить
Казалось, что комплексные числа - это просто удачный инструмент и в квантовой механике, упрощающий долгие вычисления - но при необходимости без которого можно обойтись. Но в январе 2021 года физики во главе с Марком-Оливье Рену из Института фотонных наук (ICFO) в Барселоне предложили эксперимент с несколькими источниками частиц и наблюдателями, который должен раз и навсегда установить числовое пространство квантовой механики. Они обнаружили, что в этом случае предсказания реальной и сложной формулировок различаются.
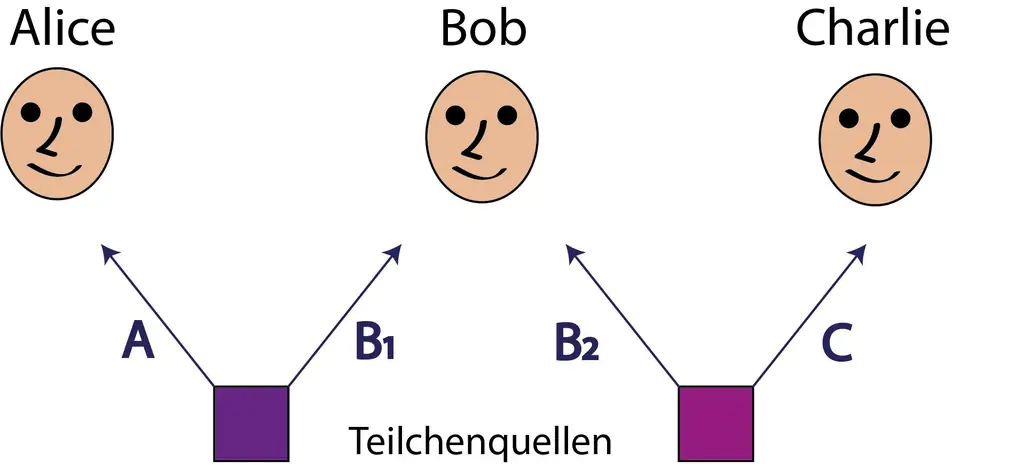
Эксперимент состоит из трех наблюдателей, Алисы, Боба и Чарли, которые выстраиваются в линию со своим измерительным оборудованием. Между Алисой и Бобом и между Бобом и Чарли находится источник, испускающий запутанные частицы. Алиса и Боб получают частицы A и B1 одновременно, и в этот момент Чарли получает C, а Боб получает B2. Алиса и Чарли могут провести конкретные измерения по своему выбору на A и C соответственно. Боб, с другой стороны, манипулирует B1 и B2 таким образом, что они затем запутываются. В результате A и C также запутались, так как ранее они были запутаны с B1 и B2..
Исход эксперимента можно предсказать с помощью комплексных чисел. Использование реального формализма дает разные результаты. Поскольку эксперимент можно реализовать при текущих технических возможностях, две рабочие группы воспользовались возможностью реализовать его в 2021 году. Группа во главе с Цзянь-Вэй Паном из Китайской академии наук использовала сверхпроводящие кубиты, а исследователи во главе с Цзиньюном Фаном из Южного университета науки и технологии в Шэньчжэне провели эксперимент с запутанными фотонами. Обе команды смогли измерить определенный параметр, который говорит нам, верна ли действительная или сложная формулировка, и оба эксперимента подтвердили сложный вариант.
Однако полностью реальное описание квантовой механики не исключается. Нет подходящей версии, например, в еще большем количестве измерений, в которой бы согласовывались сложные и реальные предсказания предлагаемого эксперимента. Однако, если вы коренным образом измените арифметические операции, такие как тензорное произведение, и, таким образом, правила вычислений квантовой физики, вы, возможно, придете к тем же результатам. Однако это было бы чрезвычайно сложно и запутанно, поэтому такой подход не особенно популярен. Это также вызовет дополнительные вопросы в других сценариях. Таким образом, теория микрокосма, по-видимому, основана на комплексных числах, а это означает, что числовое пространство, вероятно, более глубоко укоренено в природе, чем предполагалось ранее..
