Герман Минковский (1864-1909)
Минковский создал геометрическую модель неевклидова четырехмерного пространства-времени, благодаря которой специальная теория относительности Альберта Эйнштейна стала математически осязаемой.
"О, Эйнштейн? Он всегда пропускал мои лекции - я бы не поверил, что он на это способен." говорят, сказал его бывший профессор математики, когда услышал о публикации «Об электродинамике движущихся тел», которая сейчас известна как «Специальная теория относительности». Фактически, студент Альберт Эйнштейн мало интересовался абстрактной математикой, преподаваемой в Цюрихском политехническом институте (ныне ETH), о чем он позже сожалел. Процитированным профессором математики был Герман Минковский, который занимал кафедру с 1896 по 1902 год.
Герман Минковский происходил из еврейской купеческой семьи, переехавшей из Каунаса (нынешняя Литва) в Кенигсберг в 1872 году. Там мальчик посещал староместскую гимназию, несколько раз прогуливал уроки и получил аттестат зрелости в марте 1880 года - ему еще не было 16 лет. Во время учебы он познакомился с Дэвидом Гильбертом. alt="
Дружба на всю жизнь завязывается между двумя студентами и 25-летним профессором математики Адольфом Гурвицем, который переехал в Кенигсберг в 1884 году. Когда в 1881 году Парижская академия наук поставила задачу о представлении натуральных чисел в виде суммы пяти квадратов, 17-летний студент Герман Минковский настолько погрузился в доказательство гипотезы Фердинанда Готхольда Макса Эйзенштейна (1823-1852), что что он разработал из этого общую теорию, которая выходит далеко за рамки рассматриваемой темы. Хотя работа формально не соответствует требованиям конкурса (она написана на немецком языке), Минковски награждается премией Академии.
Карл Фридрих Гаусс в своих Disquisitiones Arithmeticae изложил исчерпывающую теорию бинарных квадратичных форм \(f(x, y)) с \(f(x, y)=ax^2 + bxy + cy^2), разработанная с помощью \(a, b, c \in \mathbb{Z}).
Минковский обобщает эти исследования для квадратичных форм с более чем двумя переменными. В 1885 году он получил докторскую степень, защитив диссертацию по этому вопросу. В 1887 году он получил лекцию в Боннском университете со своей докторской диссертацией «Пространственная интуиция и минимумы положительно определенных квадратичных форм». В 1892 году он был назначен экстраординарным профессором. За этим последовали два года преподавания в Кенигсберге (вслед за Гильбертом), прежде чем в 1896 году его пригласили в Швейцарский федеральный политехнический институт в Цюрихе, где с 1892 года преподавал его друг Гурвиц.
Документ «Геометрия чисел» был опубликован во время его пребывания в Цюрихе - вклад Минковского в отчет о последних достижениях в теории чисел, который он и Гильберт написали от имени Немецкой ассоциации математиков. Минковский развивает здесь идею n-мерных решеток. Эти решетки в \(mathbb{R}^n) порождены базисными векторами (например, единичными векторами); целочисленные линейные комбинации этих векторов определяют точки решетки, \(n)-мерные параллелоэдры из соседних точек определяют решетчатую сетку M.
Теорема МИНКОВСКОГО о точке решетки: дано ограниченное, выпуклое) подмножество \(T) множества \(mathbb{R}^n), которое симметрично началу координат. Если \(text{volume}(T) > 2^n \cdot \text{volume}(M)), то \(T) содержит по крайней мере еще одну точку решетки помимо начала координат.) с двумя точками \(P, Q \in T), каждая точка отрезка \(PQ) принадлежит множеству \(T)
Если вы посмотрите на обычную сетку прямоугольной декартовой системы координат в \(mathbb{R}^2), квадраты со стороной 1 образуют ячейки сетки с "объемом" 1. Для каждого подмножества \(T) с указанными выше свойствами применяется следующее: если площадь \(T) больше, чем \(2^2 \cdot 1=4), то по крайней мере один дополнительная точка сетки должна принадлежать \(T). И наоборот, для каждого эллипса, симметричного началу координат (уравнение эллипса: \(ax^2 + bxy + cy^2=d)), который не содержит дополнительных узлов решетки (как в приведенном ниже примере), площадь самое большее \(4) может быть.
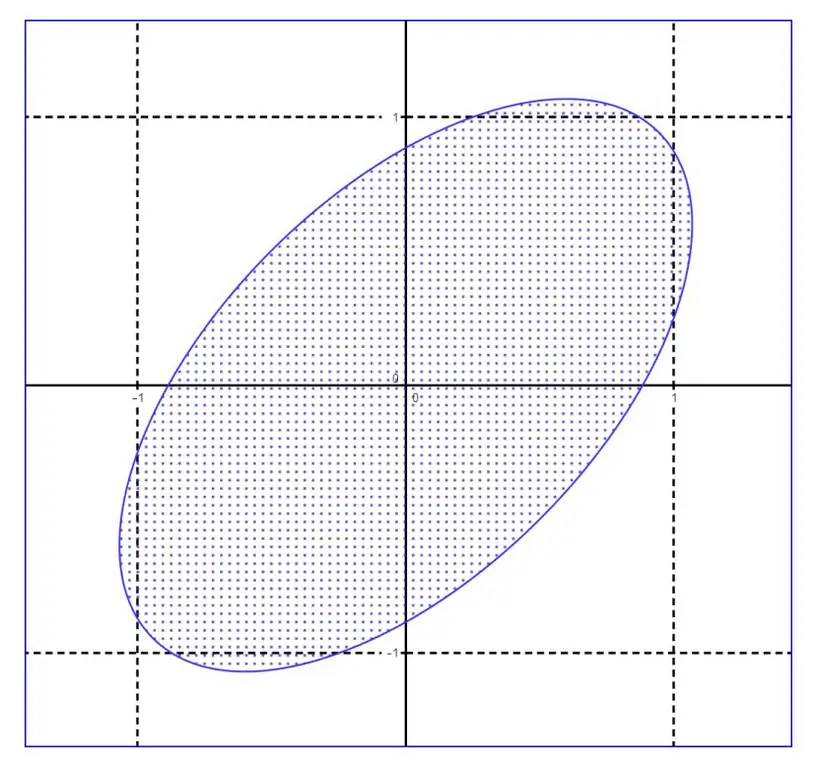
Эта теорема, по-видимому, имеющая только геометрическое значение, имеет удивительные приложения в теории чисел. Существование точек решетки (координатами которых являются целые решения) следует из условия на коэффициенты квадратичного члена, например, в следующих теоремах, найденных Эйлером: Каждое простое число вида \(6k+1 \quad (8k +1)) - это сумма квадратного числа и трехкратного (дважды) другого квадратного числа.
Работа «Геометрия чисел» содержит множество других аспектов, имеющих последствия, например, в теории числовых полей, в приближении алгебраических чисел непрерывными дробями или в связи с проблемой плотнейшей упаковки чисел. сферы. Чарльз Эрмит был так взволнован идеями книги, что, как говорят, воскликнул: «Я верю, что вижу землю обетованную», и сделал для него перевод, чтобы понять все детали работы..
1902 Минковский переезжает в созданное специально для него кресло в Геттингене, где продолжает плодотворное сотрудничество с Гильбертом. Тем временем он проявил особый интерес к проблемам теоретической физики и, среди прочего, написал энциклопедическую статью о математическом моделировании капиллярности. В 1905 году Гильберт провел семинар, посвященный электрону, открытому Йозефом Дж. Томсоном в 1897 году, и теориям, разработанным Хендриком Антоном Лоренцем и Анри Пуанкаре. С помощью преобразований Лоренца можно согласовать местоположение и время разных наблюдателей; однако теория Лоренца предполагает существование эфира. В своей теории относительности Эйнштейн предполагает, что скорость света постоянна, и может использовать это для объяснения всех явлений.
Но только Минковскому удалось проиллюстрировать идеи теории Эйнштейна. Свою знаменитую лекцию на 80-м съезде немецких естествоиспытателей и врачей в Кёльне в 1908 г. он начинает словами: «Взгляды на пространство и время, которые я хотел бы развить для вас, выросли из экспериментальной физики. В этом их сила. Их тенденция радикальна. С этого момента пространство для себя и время для себя должны полностью уйти в тень, и только некий союз между ними должен сохранять их независимость. Затем он объясняет свою геометрическую модель неевклидова 4-мерного пространства-времени, точки с координатами \((t; x; y; z)) являются событиями (время \(t) и координаты местоположения \(x, y, z)), последовательности точек мировых линий.
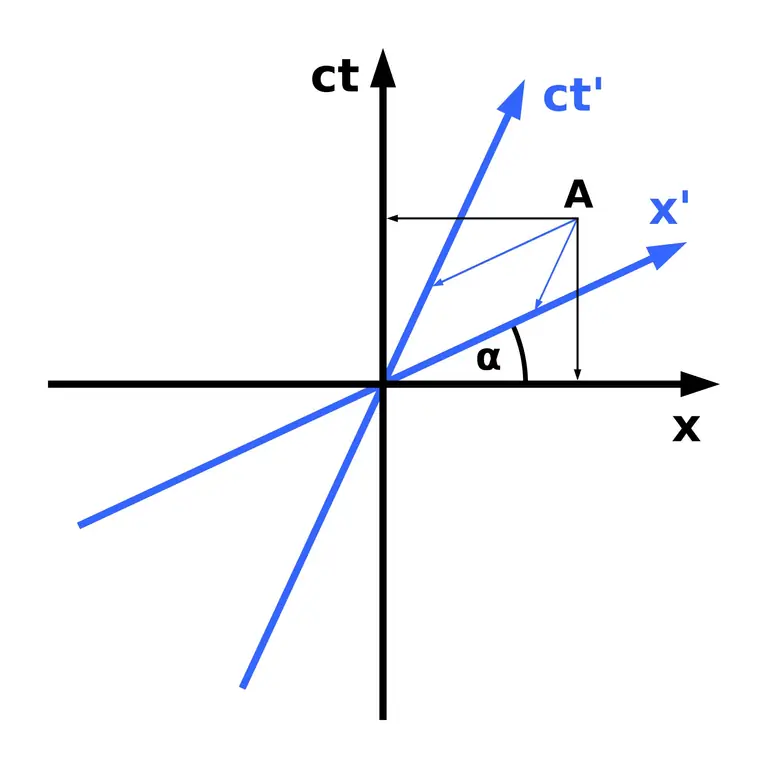
Метрика в этом векторном пространстве определяется следующим скалярным произведением двух векторов событий:
\(- (c \cdot t_1) cdot (c\cdot t_2) + x_1 \cdot x_2 + y_1 \cdot y_2 + z_1 \cdot z_2). Где \(c) - скорость света.
Для иллюстрации он строит диаграмму, на которой пространственные координаты представлены только одной осью. С помощью этого упрощения можно понять кажущиеся парадоксальными явления, такие как замедление времени или сокращение длины. С помощью трехмерного представления двойного светового конуса он объясняет, что означают прошлое и будущее с точки зрения наблюдателя.
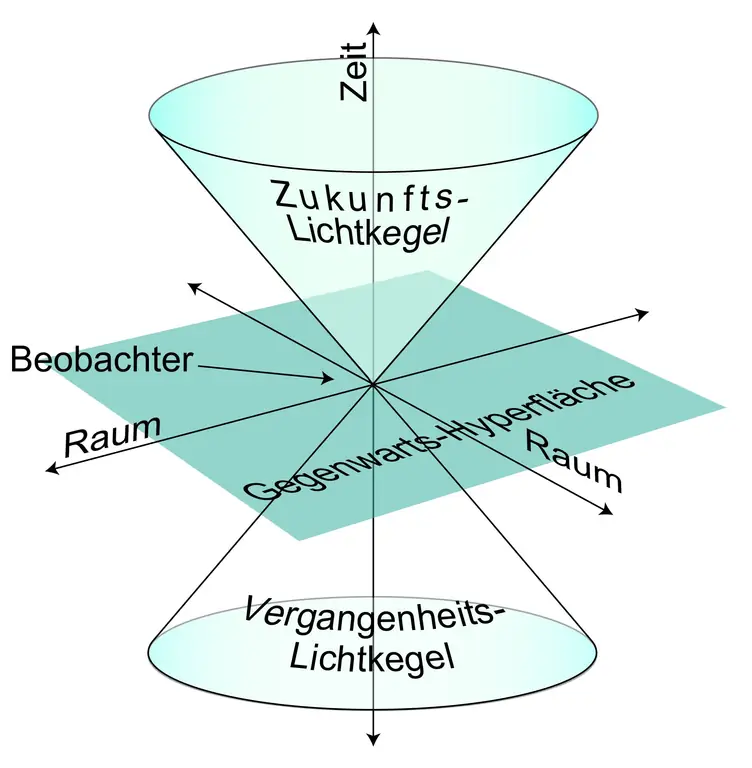
Эйнштейн поначалу не был в особом восторге от математической модели Минковского (с тех пор, как математики ухватились за теорию относительности, я уже сам ее не понимаю), но позже признает, что без этого подхода… общая теория относительности могла бы быть в подгузниках застрял.
Когда Минковский умирает в возрасте всего 44 лет после аппендэктомии, Гильберт произносит поминальную речь, полную благодарности другу, который предложил ему это в 1900 году, в своей лекции в Париже на Международном конгрессе математиков заглянуть в будущее: какие проблемы будут решать математики в ближайшие десятилетия? - лекция, которая до сих пор играет роль в математических исследованиях.
